I haven’t had much look tackling the pendulum balancing problem with Q-learning.  It seems that there are many states in the system, and the output (motor speed) should really be a continuous variable, that it didn’t work well, with the Q-learner that spits out discrete speeds, or even generate faster, stay, slower discretised states.

The problem is that by using conventional gradient descent methods common in deep learning, we are trying to ‘solve’ the weights of a neural network in such a way that the network learns how the transfer function of a system works, ie, predict the output of a system given some input, rather than trying to find a strategy.  While this may certainly be useful in modelling how physical systems like the pendulum works, in the sense that it predicts the orientation/velocities at the next time step given the variables of the current state, it may not be able to come up with a strategy to how to get to a certain desired state, especially when the current state (say the pendulum is inverted completely) is so far away from the desired state 180 degrees away.  Not to mention that it’s got to stay up there once it swings all the way up.

I’ve began to question the idea to use SGD / back-propagation to train networks to achieve tasks, as there may be too many local minimums.  In addition, I think the Q-learning algorithm described in the atari paper essentially hacks the memory element into a feed-forward network system.  The main contribution from that paper is essentially the use of convolutional networks processing video game images, and having the back-prop work all the way from expected reward down to features extracted during convolution, so it can work very fast on GPUs.  I am thinking the more correct approach is to bite the bullet and use recurrent neural networks that can incorporate feedback and memory elements for task-based training.  This may make it very difficult to train the recurrent networks using SGD / backprop.  We don’t even really know what desired output we want the network to generate given the current input state.

source: wikipedia

During the evenings, I have been reading up on using genetic algorithm approaches to train neural networks.  The field seems to be studied in great depth at the University of Texas, and the Swiss AI Lab‘s work on RNNs, and strangely I haven’t heard about much of this work at Stanford or University of Toronto (my alma mater!) or NYU so much with all the buzz about deep learning.

A good introduction to the field I found was on these slides at the U of Texas NN lab.  Digging through some older thesis publications, I found John Gomez’s thesis extremely helpful and well written, and as someone who has not implemented a Genetic Algorithm before, the pseudocode in the thesis put things to light on how this stuff works.

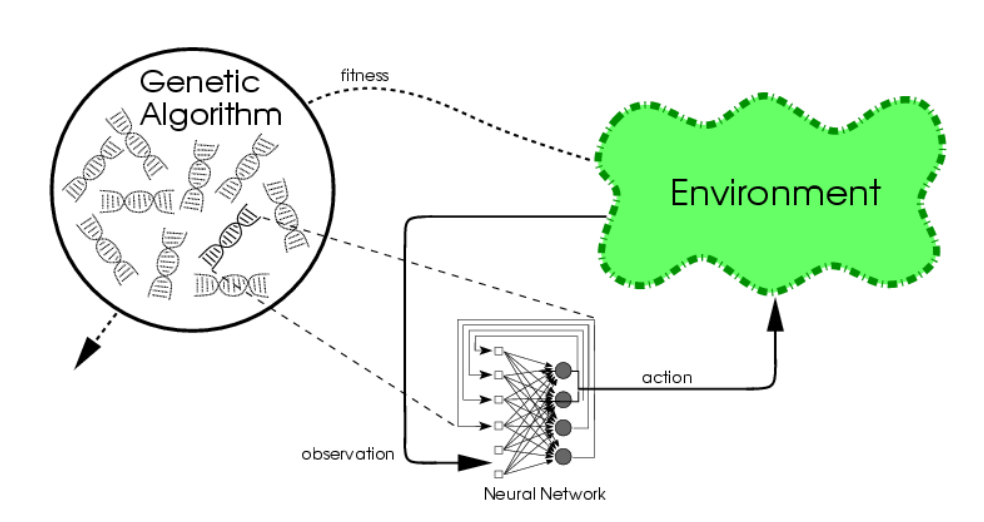
I realised that these methods may be superior to Q-learning or backprop based to search for a strategy that requires a sequence of multiple actions.  Even the simplest neuroevolution algorithm (‘conventional neuroevolution’), the plain vanilla algorithm with no extra bells and whistles, maybe able to solve many interesting problems.  What this simple algorithm does is:

1. Take a certain neural network architecture, feed forward, or even recurrent, and make N number (say 100) of these neural nets each randomised with different weights.

2. Try to accomplish the task at hand (balance the pendulum), for each of the 100 networks, and then score how well each performs the task (assign the score of say the average angle squared during the life of the task, where zero degree is upright)

3. Sort the networks by scores achieved, and keep the top 20 networks, and throw the rest away.  For each network, dump all the weights and biases into a one-dimensional array of floats, in a consistent orderly way, and call that the chromosome of the network.

4. Generate 80 new chromosomes by mixing and matching the top 20 network’s chromosomes by performing simple random crossover and mutation.  The theory is that the ‘good stuff’ of how stuff should be done should be embedded in the chromosomes of the winners, and by combining the weights of the winners to generate new chromosomes, the hope is the ‘offsprings’ will also be good, or better than the parents.  From these 80 new chromosomes, generate 80 new networks.

5. Repeat tasks (2) -> (4) until the desired score of the best network is somewhat satisfactory.

crossover and mutation example

That’s the gist of the CNE algorithm.  It solves a big problem where we can easily define and score the goal, and not worry about backprop and what target values to train.  We can simply use the above algorithm to generate a motor speed for each time step and supply the network with current orientation/velocity states, and watch it search the solution space to find one that is satisfactory.  I like this method more in systems that contains many local maximums, so for SGD you just end up with the local maximum, while the NE algorithms has a better chance to find a much better local, or even global maximum.  In addition, it is relatively simple to incorporate recurrent neural network structures using CNE.

There are still many problems with CNE in the literature, where the algorithm actually loses diversity and converges also to a local maximum solution, and much of the work in this subfield is to find more advanced algorithms (in the thesis above, ESP and NEAT are named).

I will try to hack convnet.js and implement a simple CNE trainer that can train a network to achieve some score, and put it to test later to see if the pendulum problem may be attacked using these methods.