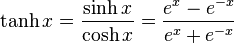Recurrent neural network playing slime volleyball. Can you beat them?
I remember playing this game called slime volleyball, back in the day when Java applets were still popular. Although the game had somewhat dodgy physics, people like me were hooked to its simplicity and spent countless hours at night playing the game in the dorm rather than getting any actual work done.
As I can’t find any versions on the web apart from the old antiquated Java applets, I set out to create my own js+html5 canvas based version of the game (complete with the unrealistic arcade-style ‘physics’). I set out to also try to apply the genetic algorithm coded earlier to train a simple recurrent neural network to play slime volleyball. Basically, I want to find out whether even a simple conventional neuroevolution techniques can train a neural network to become an expert at the this game, before exploring more advanced methods such as NEAT.
The first step was to write a simple physics engine to get the ball to bounce off the ground, collide with the fence, and with the players. This was done using the designer-artist-friendly p5.js library in javascript for the graphics, and some simple physics math routines. I had to brush up the vector maths to get the ball bouncing function to work properly. After this was all done, the next step was to add in keyboard / touchpad so that the players can move and jump around, even when using a smartphone / tablet.
The fun and exciting part was to create the AI module to control the agent, and to see whether it can become good at playing the game. I ended up using basic CNE method implemented earlier, as an initial test, to train a standard recurrent neural network, hacked together using the convnet.js library. Below is a diagram of the recurrent network we will train to play slime volleyball, where the magic is done:
The inputs of the network would be the position and velocity of the agent, the position and velocity of the ball, and also of the opponent. The output would be three signals that would trigger the ‘forward’, ‘backward’, and ‘jump’ controls to be activated. In addition, an extra 4 hidden neurons would act as hidden state and fed back to the input, this way it is essentially an infinitely deep feed forward neural network, and potentially remember previous events and states automatically in the hopes of being able to formulate more complicated gameplay strategies. One thing to note is that the activation functions would fire only if the signal is higher than a certain threshold (0.75).
I also made the agent’s states be the same independent of whether the agent was playing on the left or the right hand side of the fence, by having their locations be relative to the fence, and the ball positions adjusted accordingly according to which side they were playing in. That way, a trained agent can use the same neural network to play on either side of the fence.
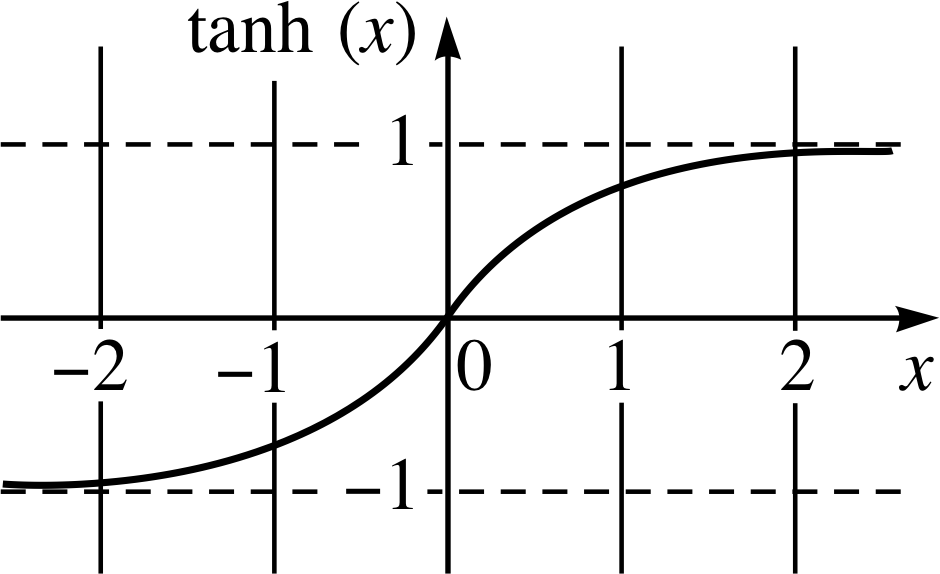
Rather than using the sigmoid function, I ended up using the hyperbolic tangent (tanh) function to control the activations, which convnet.js supports.
The tanh function is defined as:
The tanh function can be a reasonable activation function for a neural network, as it tends towards +1 or -1 when the inputs get steered one way or the other. The x-axis would be the game inputs, such as the locations and velocities of the agent, the ball, and the opponent (all scaled to be +/- 1.0 give or take another 1.0) and also the output and hidden states in the neural network (which will be within +/- 1.0 by definition).
As velocities and ball locations can be positive or negative, this may be more efficient and a more natural choice compared to the sigmoid. As explained earlier, I also scaled my inputs so they were all in the order of +/- 1.0 size, similar to the output states of the hidden neurons, so that all inputs to the network will have roughly the same orders of magnitude in size on average.
Training such a recurrent neural network involves tweaks on the genetic algorithm trainer I made earlier, since there’s really no fitness function that can return a score, as either one wins or loses a match. What I ended up doing is to write a similar training function that gets each agent in the training population to play against other agents. If the agent wins, its score increases by one, and decreases by one if it loses. On ties (games that longer than the equivalent of 20 real seconds in simulation), no score is added or deducted. Each agent will play against 10 random agents in the population in the training loop. The top 20% of the population is kept, the rest discarded, and crossover and mutations are performed for the next generation. This is referred to as the ‘arms race’ method to train agents to play a one-on-one game.
By using this method, the agents did not need to be programmed by hand any heuristics and rules of the game, but will simply explore the game and figure out how to win. And the end result suggests that they seem to be quite good at it, after a few hundred generations of evolution! Check out the demo of the final result below on the youtube video.
The next step can be employ more advanced methods such as NEAT, or ESP for the AI, but that can be overkill for a simple pong-line game. It is also a candidate for applying the Deep Q-Learner already built in convnetjs, as the game playing strategy is quite simple. For now I think I have created a fairly robust slime volleyball player that is virtually impossible to beat by a human player consistently.
Try the game out yourself and see if you can beat it consistently. It works on both desktop (keyboard control), or smartphone / tablet via touch controls. Desktop version is easier to control either via keyboard arrows or mouse dragging. Feel free to play around with the source on github, but apologies if it’s not the neatest structured code as it is intended to be more of a sketch rather than a proper program.
Update (13-May-2015)
This demo at one point got to the front page of Y Combinator’s Hacker News. I made another demo showing the evolution of Agent’s behaviour over time, from knowing nothing at the beginning. Please see this post for more information.
Citation
If you find this work useful, please cite it as:
@article{ha2015slimevolley,
title = "Neural Slime Volleyball",
author = "Ha, David",
journal = "blog.otoro.net",
year = "2015",
url = "https://blog.otoro.net/2015/03/28/neural-slime-volleyball/"
}