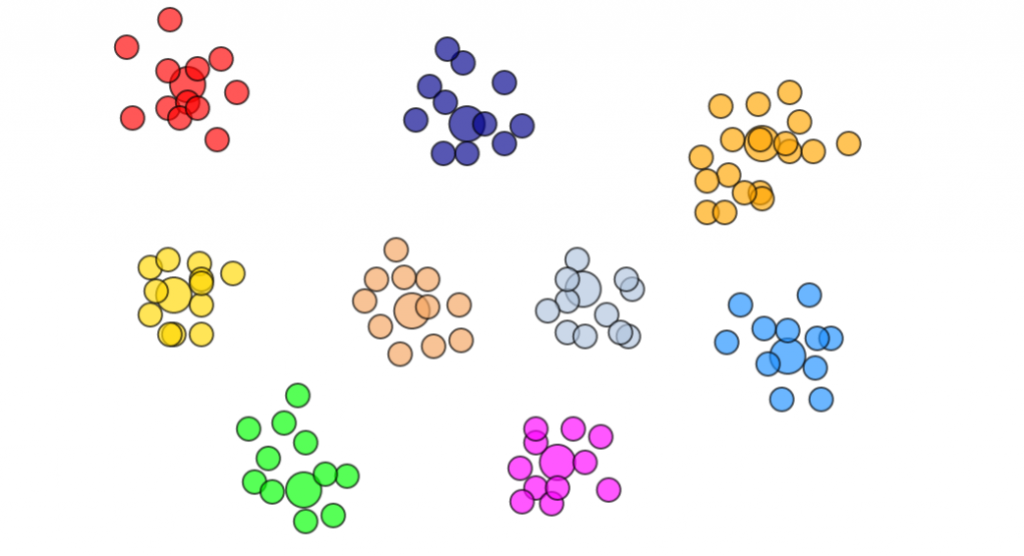
k-medoids clustering demo

I found that the way the NEAT algorithm does speciation to be rather arbitrary, and implementing that process seems like creating a jungle filled with unicorns.  I find myself questioning why certain things are done certain ways without much justification in certain implementations.  There’s got to be a way to do speciation in a structured and well defined way like K-means clustering.  I wanted to try K-means clustering for this task but obviously it wouldn’t work as each genome cannot be mapped elegantly to an N-dimensional vector.

Currently experimenting with the alternative algorithm called k-medoids that can handle clustering in the absence of coordinate information.  All it requires is that there is a distance function that can return a real number when defining some distance between each element.  How it works is that it randomly chooses K elements from the list of all elements (the ‘medoids’), and clusters each other element to the nearest medoid.  We would compute a cost function that is the total distance for each non-medoid to its medoid.  Iteratively then we would swap non-medoid elements with medoid elements to try to minimise this distance cost function.

I found it worked quite well after I tried to code up a simple JS demo to try to cluster from 1 to 9 groups.  The largest circle represent the medoid in each group.